Post History

Maxwell equations EM wave confusion

The general formula for a EM wave (solving for the E field) is:

![](https://physics.codidact.com/uploads/5PPqUrHwND5jdpVT72cJqXZs)

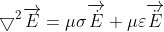
where 

$\varepsilon  = \varepsilon _{r}+j\frac{\sigma }{\omega }$

My professor told me that the conductivity of vacuum is 0 so we eliminate the term with the $\sigma $ so we get the [wave equation](https://en.wikipedia.org/wiki/Wave_equation).

He also told me that when the material is a conductor the term with the first derivative of the electric field with respect to time dominates and the term with the second derivative is negligible so we can approximate the solution using the solutions for the [diffusion equation](https://en.wikipedia.org/wiki/Diffusion_equation).

However doesnt the term of the second derivate have a imaginary part ($j\frac{\sigma}{\omega}$) which is very big?Or $\varepsilon $ in the general equation is only the real part of the electric permeability ?