Post History
How to derive the Lagrangian differential force? $$\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})+\frac{\partial L}{\partial x}=0$$ I was trying to do something. $$L=T-U=\frac{1}{2} m\dot{x}^...
#3: Post edited
- How to derive the Lagrangian differential force?
- $$\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})+\frac{\partial L}{\partial x}=0$$
- I was trying to do something.
- $$L=T-U=\frac{1}{2} m\dot{x}^2-\frac{1}{2}kx^2$$
- $$\frac{\partial L}{\partial \dot{x}}=m\dot{x}$$
- $$\frac{\partial L}{\partial x}=-kx$$
- $$\frac{d}{dt}\frac{\partial L}{\partial \ddot{x}}=m\ddot{x} (t)$$
- So, I can write that
- $$m\ddot{x}(t)+kx$$
But, how can I prove that it's equal to $0$. I should find the equation from somewhere else. What's that?
- How to derive the Lagrangian differential force?
- $$\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})+\frac{\partial L}{\partial x}=0$$
- I was trying to do something.
- $$L=T-U=\frac{1}{2} m\dot{x}^2-\frac{1}{2}kx^2$$
- $$\frac{\partial L}{\partial \dot{x}}=m\dot{x}$$
- $$\frac{\partial L}{\partial x}=-kx$$
- $$\frac{d}{dt}\frac{\partial L}{\partial \ddot{x}}=m\ddot{x} (t)$$
- So, I can write that
- $$m\ddot{x}(t)+kx$$
- But, how can I prove that it's equal to $0$. I should find the equation from somewhere else. What's that?
- >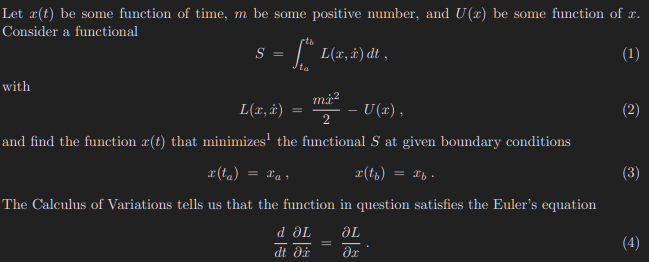 ~ https://people.umass.edu/~bvs/601_Lagrange.pdf <br/> Which Euler's equation?
#2: Post edited
- How to derive the Lagrangian differential force?
- $$\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})+\frac{\partial L}{\partial x}=0$$
- I was trying to do something.
- $$L=T-U=\frac{1}{2} m\dot{x}^2-\frac{1}{2}kx^2$$
- $$\frac{\partial L}{\partial \dot{x}}=m\dot{x}$$
- $$\frac{\partial L}{\partial x}=-kx$$
- $$\frac{d}{dt}\frac{\partial L}{\partial \ddot{x}}=m\ddot{x} (t)$$
- So, I can write that
$$m\ddot{x}(t)-kx$$- But, how can I prove that it's equal to $0$. I should find the equation from somewhere else. What's that?
- How to derive the Lagrangian differential force?
- $$\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})+\frac{\partial L}{\partial x}=0$$
- I was trying to do something.
- $$L=T-U=\frac{1}{2} m\dot{x}^2-\frac{1}{2}kx^2$$
- $$\frac{\partial L}{\partial \dot{x}}=m\dot{x}$$
- $$\frac{\partial L}{\partial x}=-kx$$
- $$\frac{d}{dt}\frac{\partial L}{\partial \ddot{x}}=m\ddot{x} (t)$$
- So, I can write that
- $$m\ddot{x}(t)+kx$$
- But, how can I prove that it's equal to $0$. I should find the equation from somewhere else. What's that?
#1: Initial revision
Prove differential form of Lagrangian
How to derive the Lagrangian differential force?
$$\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})+\frac{\partial L}{\partial x}=0$$
I was trying to do something.
$$L=T-U=\frac{1}{2} m\dot{x}^2-\frac{1}{2}kx^2$$
$$\frac{\partial L}{\partial \dot{x}}=m\dot{x}$$
$$\frac{\partial L}{\partial x}=-kx$$
$$\frac{d}{dt}\frac{\partial L}{\partial \ddot{x}}=m\ddot{x} (t)$$
So, I can write that
$$m\ddot{x}(t)-kx$$
But, how can I prove that it's equal to $0$. I should find the equation from somewhere else. What's that?


















