Post History
We have place a charged particle of 2C with mass 2kg, 1mm above a current-carrying wire of 1A.The charged particle has an initial velocity of 100m/s The magnetic field of the wire for simplicity w...
#3: Post edited
by
MissMulan
·
2021-08-10T21:56:18Z (over 3 years ago)
- We have place a charged particle of 2C with mass 2kg, 1mm above a current-carrying wire of 1A.The charged particle has an initial velocity of 100m/s
- How can we find the equation of motion of the particle? The force acting on it will be changing because it will move away from the wire and the angle between the particle's velocity with the magnetic field will change as well?
- 
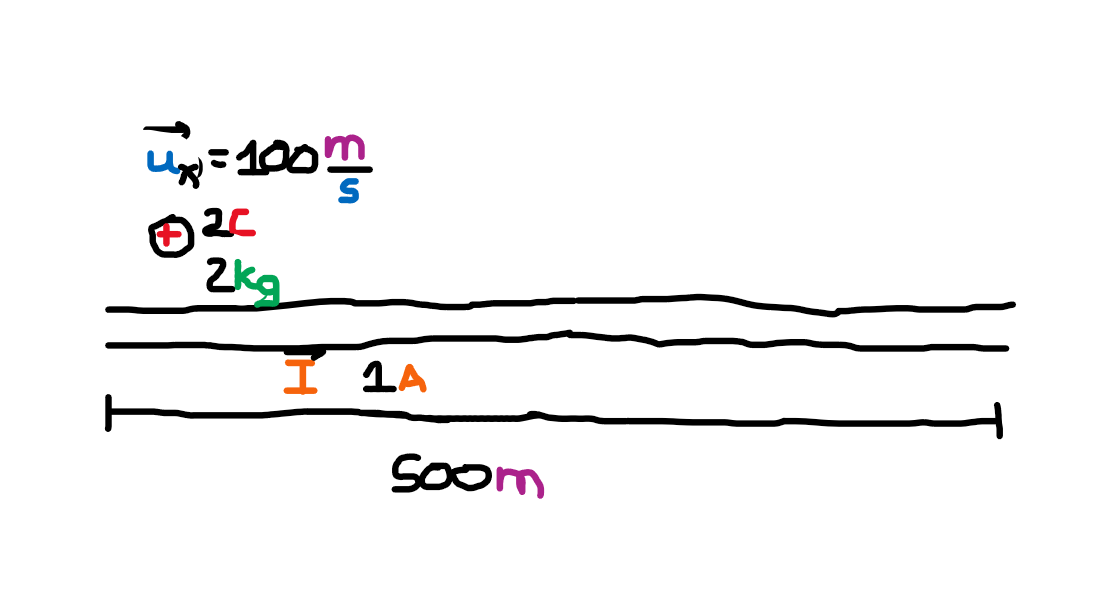
- I thought to find the time the particle spends inside the magnetic field
- $$d = u\times t \implies t = \frac{d}{u} = 5\\,\text{s}$$
- but in order to integrate with respect to t I have to find how the distance from the wire changes as time passes and the relationship between time and the angle between the velocity and the magnetic field which are pretty hard and i am stuck. How do I continue?
- We have place a charged particle of 2C with mass 2kg, 1mm above a current-carrying wire of 1A.The charged particle has an initial velocity of 100m/s
- The magnetic field of the wire for simplicity will exist as long as we are only over the wire.
- How can we find the equation of motion of the particle? The force acting on it will be changing because it will move away from the wire and the angle between the particle's velocity with the magnetic field will change as well?
- 
- I thought to find the time the particle spends inside the magnetic field
- $$d = u\times t \implies t = \frac{d}{u} = 5\\,\text{s}$$
- but in order to integrate with respect to t I have to find how the distance from the wire changes as time passes and the relationship between time and the angle between the velocity and the magnetic field which are pretty hard and i am stuck. How do I continue?
#2: Post edited
by
Mithrandir24601
·
2021-08-09T21:54:22Z (over 3 years ago)
fixed Latex formatting
We have place a charged particle of 2C with mas 2kg 1mm above a current-carrying wire of 1A.The charged particle has an initial velocity of 100m/sHow can we find the equation of motion of the particle?The force acting on it will be changing because it will move away from the wire and the angle between the particle's velocity with the magnetic field will change as well?- I thought to find the time the particle spends inside the magnetic field
but in order to integrate with respect to t I have to find how the distance from the wire changes as time passes and the relationship between time and the angle between the velocity and the magnetic field which are pretty hard and i am stuck.How do I continue
- We have place a charged particle of 2C with mass 2kg, 1mm above a current-carrying wire of 1A.The charged particle has an initial velocity of 100m/s
- How can we find the equation of motion of the particle? The force acting on it will be changing because it will move away from the wire and the angle between the particle's velocity with the magnetic field will change as well?
- 
- I thought to find the time the particle spends inside the magnetic field
- $$d = u\times t \implies t = \frac{d}{u} = 5\\,\text{s}$$
- but in order to integrate with respect to t I have to find how the distance from the wire changes as time passes and the relationship between time and the angle between the velocity and the magnetic field which are pretty hard and i am stuck. How do I continue?
#1: Initial revision
by
MissMulan
·
2021-07-31T23:48:09Z (over 3 years ago)
Motion of charged particle inside a magnetic field
We have place a charged particle of 2C with mas 2kg 1mm above a current-carrying wire of 1A.The charged particle has an initial velocity of 100m/s How can we find the equation of motion of the particle?The force acting on it will be changing because it will move away from the wire and the angle between the particle's velocity with the magnetic field will change as well?  I thought to find the time the particle spends inside the magnetic field  but in order to integrate with respect to t I have to find how the distance from the wire changes as time passes and the relationship between time and the angle between the velocity and the magnetic field which are pretty hard and i am stuck.How do I continue