Post History
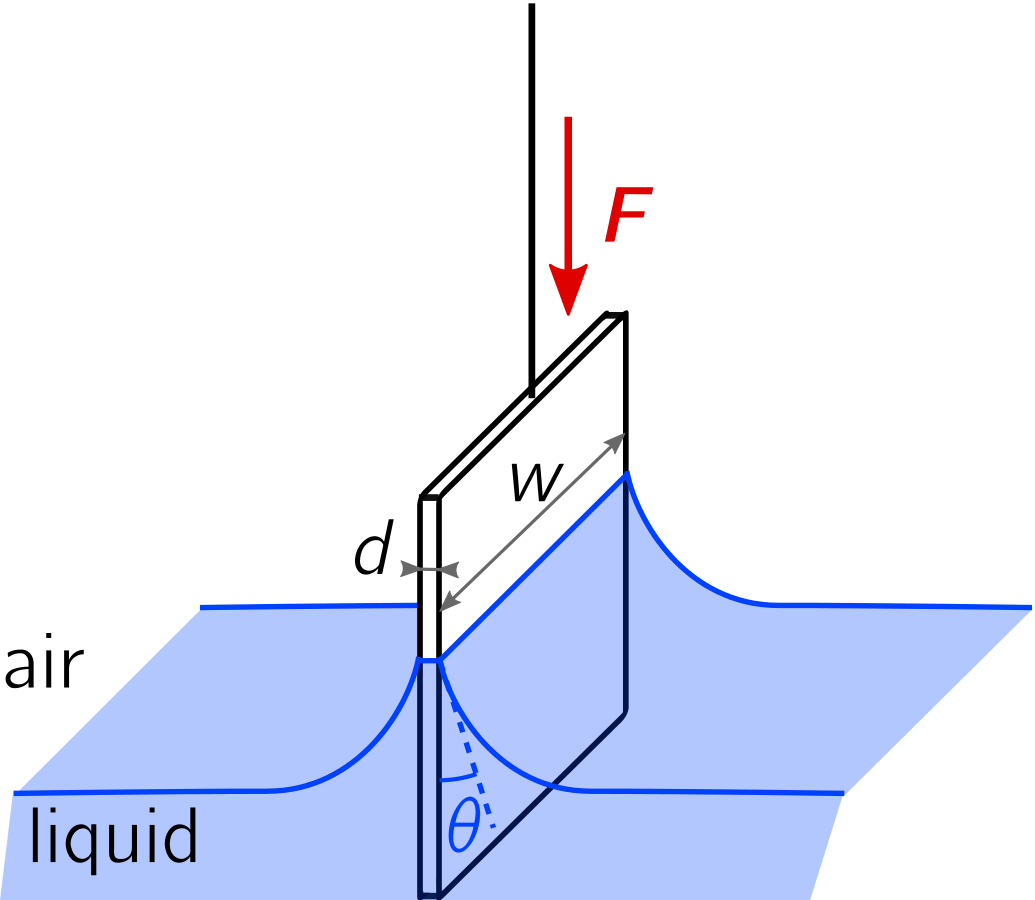
Let's say we have a single plate with liquid on both sides rising up due to surface tension. The meniscus formed has a radius of curvature $R$. I'm trying to find the excess pressure, i.e, the pre...
#1: Initial revision
Applying Young-Laplace equation on meniscus formed due to rise of liquid on a single plate
Let's say we have a single plate with liquid on both sides rising up due to surface tension. The meniscus formed has a radius of curvature $R$.
I'm trying to find the excess pressure, i.e, the pressure difference between the exterior and interior of the meniscus.
Since there is only one curved surface (the meniscus which extends across the length of the plate) whose radius of curvature is $R$, from the Young-Laplace equation, the excess pressure should be
$$\triangle P = \frac{\gamma}{R}$$
where $\gamma$ is the surface tension.
However, I know that the excess pressure should be
$$\triangle P = \frac{2 \gamma}{R}$$
The only way we get the factor of $2$ is if there are two curved surfaces with radius $R$. I'm new to using the Young-Laplace equation, and I just don't understand how there are two curved surfaces with radius $R$. I'm somewhat sure that the two meniscus' on either sides of the plate aren't the two curved surfaces since the plate is dividing them and they have no contact.
Here's an [image](https://en.wikipedia.org/wiki/Wilhelmy_plate) which shows what kind of a setup I'm referring to (credits: Vincent Émyde)